---

MOSFET

Metal
Oxide
Semiconductor
Field
Effect
Transistor

Operation Regions

Transition point

• NMOS: \(V_{DS} (sat) = V_{GS} - V_{TN}\)
• PMOS: \(V_{SD} (sat) = V_{SG} - V_{TP}\)

Operation Region	NMOS	PMOS
Saturation	\(i_D = K_n (V_{DS}(sat))^2\)	\(i_D = K_n (V_{SG}(sat))^2\)
Triode	\(i_D = K_n (2V_{DS}(sat) \times V_{DS} - V^2_{DS})\)	\(i_D = K_n (2V_{SG}(sat) \times V_{SD} - V^2_{SD})\)
Cutoff	\(i_D = 0\)	\(i_D = 0\)

Condition	NMOS	PMOS
Saturation	\(V_{DS} \geq V_{DS}(sat)\)	\(V_{SD} \geq V_{SD}(sat)\)
Triode	\(V_{DS} < V_{DS}(sat)\)	\(V_{SD} < V_{SD}(sat)\)
Cutoff	\(V_{GS} < V_{TN}\)	\(\lvert V_{SG} \rvert < \lvert V_{TP} \rvert\)

Ideally, we want NMOS and PMOS to be in saturation mode.

Solving Process

1. Assume operation region (default: saturation)
2. Analyze following saturation model, get \(i_D, V_{DS}\)
3. Verify conditions for assumed region are met: \(V_{DS} \geq V_{DS}(sat)\)
   • If yes, analysis is complete.
   • If not, change operation region and analyze again.

---

Remember: Current does NOT flow into the gate:

\[i_G = 0\]

---

Below are some examples for circuits. Here, KVL is your best friend. You can easily get this equations with KVL.

NMOS

The symbol is not an NMOS but the renderer does not have it (to change !important).

Assume \(V_{DD},\ V_{TN},\ K_n\) and the resistor values are given.

\[V_{GS} = V_G - V_S,\ V_S = 0\] \[V_{GS} = V_G = \frac{R2}{R1 + R2} V_{DD}\]

If \(V_{GS} \leq V_{TN}\), then the NMOS is in the cutoff region, \(i_D = 0,\ V_{DS} = V_{DD}\).

If not, continue:

\[V_{DS}(sat) = V_{GS} - V_{TN}\]

Assume \(V_{DS} \geq V_{DS}(sat)\):

\[i_D = K_n (V_{DS}(sat))^2\] \[V_{DS} = V_{DD} - i_D R_D\]

If \(V_{DS} \geq V_{DS}(sat)\), then the NMOS is indeed in saturation, the analysis is complete.

If not, then the NMOS is in triode region:

\[i_D = K_n (2V_{DS}(sat) \times V_{DS} - V^2_{DS})\] \[V_{DS} = V_{DD} - i_D R_D\]

With the new value of \(V_{DS}\), verify that \(V_{DS} < V_{DS}(sat)\). If yes, analysis is complete.

If not, verify your calculations.

PMOS

Assume \(V_{DD},\ V_{TP},\ K_n\) and the resistor values are given.

\[V_{SG} = \frac{R1}{R1 + R2} V_{DD}\]

If \(\lvert V_{SG} \rvert < \lvert V_{TP} \rvert\), then the PMOS is in the cutoff region, \(i_D = 0,\ V_{SD} = V_{DD}\).

If not, continue:

\[V_{SD}(sat) = V_{SG} + V_{TP}\]

Assume \(V_{SD} \geq V_{SD}(sat)\):

\[i_D = K_n (V_{SG}(sat))^2\] \[V_{SD} = V_{DD} - i_D R_D\]

If \(V_{SD} \geq V_{SD}(sat)\), then the PMOS is indeed in saturation, the analysis is complete.

If not, then the PMOS is in triode region:

\[i_D = K_n (2V_{SD}(sat) \times V_{SD} - V^2_{SD})\] \[V_{SD} = V_{DD} - i_D R_D\]

With the new value of \(V_{DS}\), verify that \(V_{DS} < V_{DS}(sat)\). If yes, analysis is complete.

If not, verify your calculations.

NMOS, PMOS Logic gates

See Logic Gates with MOSFETs

---

BJT

Bipolar
Junction
Transistor

Remember p-n junctions? BJTs consist of:

• npn
• pnp

Operation Regions

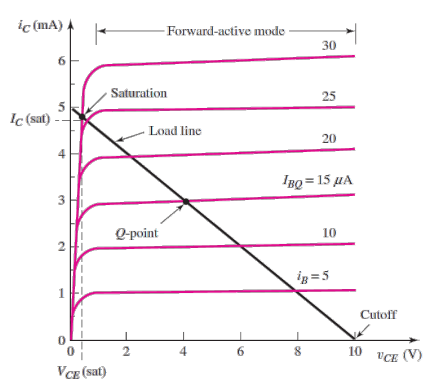
Transition point

• NPN: \(V_{CE} (sat)\) (Usually 0.2 V)
• PNP: \(V_{EC} (sat)\)

Operation Region	NPN	PNP
Saturation	\(V_{CE} = V_{CE}(sat)\)	\(V_{EC} = V_{EC}(sat)\)
Forward Bias	\(i_C = \beta i_B\)	\(i_C = \beta i_B\)
Cutoff	\(i_C = 0,\ i_B = 0\)	\(i_C = 0,\ i_B = 0\)

Condition	NPN	PNP
Saturation	\(\beta i_B > i_C\)	\(\beta i_B > i_C\)
Forward Bias	\(V_{CE} > V_{CE}(sat)\)	\(V_{EC} > V_{EC}(sat)\)
Cutoff	\(V_{BE} < V_{BE}(on)\)	\(V_{EB} < V_{EB}(on)\)

In forward bias:

\[i_C = \beta i_B = \alpha i_E\] \[i_E = i_B + i_C\] \[i_E = (1 + \beta) i_B\] \[\alpha = \frac{\beta}{1 + \beta}\]

Solving Process

1. Assume operation region (default: forward bias)
2. Analyze following forward-bias model, get \(i_B,\ i_C,\ i_E,\ V_{CE}\)
3. Verify conditions for assumed region are met: \(V_{CE} \geq V_{CE}(sat)\)
   • If yes, analysis is complete.
   • If not, change operation region and analyze again.

Below are some examples:

NPN

• Collector: Input
• Base: Input
• Emitter: Output

The circuit above can be replaced by an equivalent linear circuit assuming forward bias, where the transistor becomes:

• A dependent current source \(\beta i_B\) from the Collector to the Emitter
• A diode pointing from the Base to the Emitter with \(v_{\gamma} = V_{BE}(on)\)

Assume \(V_{B},\ V_{CC},\ V_{BE}(on),\ \beta\) and the resistor values are given.

\[i_B = \frac{V_{B} - V_{BE}(on)}{R_B}\]

If \(i_B < 0\), the NPN is cutoff.

If not, continue:

\[i_C = \beta i_B\] \[V_{CE} = V_{CC} - i_C R_C\]

If \(V_{CE}(sat)\) is given and \(V_{CE} > V_{CE}(sat)\), the NPN is in forward-bias and the analysis is complete.

If not, the NPN is in saturation:

\[V_{CE} = V_{CE}(sat)\] \[i_C = \frac{V_{CC} - V_{CE}(sat)}{R_C}\]

If \(i_C < \beta i_B\), the analysis is complete. If not, verify your calculations.

PNP

• Collector: Output
• Base: Output
• Emitter: Input

The circuit above can be replaced by an equivalent linear circuit assuming forward bias, where the transistor becomes:

• A dependent current source \(\beta i_B\) from the Emitter to the Collector
• A diode pointing from the Emitter to the Base with \(v_{\gamma} = V_{EB}(on)\)

Assume \(V_{B},\ V_{CC},\ V_{EB}(on),\ \beta\) and the resistor values are given.

\[i_B = \frac{V_{B} - V_{EB}(on)}{R_B}\]

If \(i_B < 0\), the PNP is cutoff.

If not, continue:

\[i_C = \beta i_B\] \[V_{EC} = V_{CC} - i_C R_C\]

If \(V_{EC}(sat)\) is given and \(V_{EC} > V_{EC}(sat)\), the PNP is in forward-bias and the analysis is complete.

If not, the PNP is in saturation:

\[V_{EC} = V_{EC}(sat)\] \[i_C = \frac{V_{CC} - V_{EC}(sat)}{R_C}\]

If \(i_C < \beta i_B\), the analysis is complete. If not, verify your calculations.

Voltage dividers

Instead of two independent volt sources, \(V_{CC}\) can be arranged with a pair of resistors to divide the voltage in the Base:

The voltage and current at the base can be obtained with a Thévenin equivalent:

Where:

\[R_{TH} = R_1 \| R_2 = \frac{R_1 R_2}{R_1 + R_2}\] \[V_{TH} = \frac{R_2}{R_1 + R_2} V_{CC}\]

Then the analysis is the same as before.

BJT Logic Gates

See Logic Gates with BJTs

Amplifiers

See amplifiers here