Home

윤志

[云 ~ 찌]

Induction Motors

Motors

date: 2025-04-15

Induction Motors

Speed of Magnetic Field

\[n_{\text{sync}} = \frac{120 f_{\text{se}}}{P}\]

Where

  • \(f_{\text{se}}\): Stator frequency in Hz
  • \(P\): Number of poles

Slip

\[s = \frac{n_{\text{sync}} - n_m}{n_{\text{sync}}}\]

Where

  • \(s\): slip
  • \(n_{\text{sync}}\): speed of magnetic fields
  • \(n_{m}\): mechanical shaft speed

In terms of angular velocity \(\omega\),

\[s = \frac{ {\omega}_{\text{sync}} - {\omega}_m }{ {\omega}_{\text{sync}} }\]

Rotor Frequency

\[f_{\text{re}} = sf_{\text{se}}\] \[f_{\text{re}} = \frac{P}{120} \left(n_{\text{sync}} - n_m \right)\]

Shaft Load Torque

\[{\tau}_{\text{load}} = \frac{P_{out}}{ {\omega}_m}\]

Induction Motor Equivalent Circuit

Per-phase equivalent

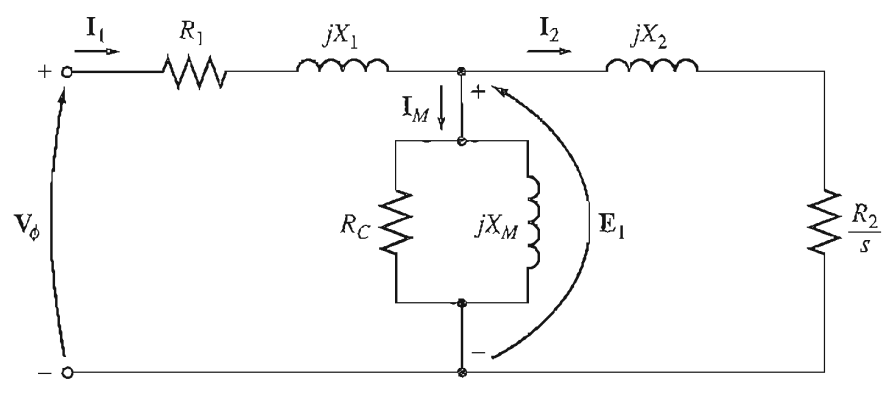
image

  • \(R_1\): Stator resistance
  • \(X_1\): Stator leakage reactance
  • \(R_C\): Core resistance?
  • \(X_M\): Magnetizing reactance
  • \(R_2\): Rotor resistance
  • \(X_2\): Rotor leakage reactance
  • \(E_1\): Applied voltage, internal stator voltage
  • \(V_{\phi}\): Input voltage to a phase

Power

Power losses to consider:

  • Stator copper loss
  • Stator core loss
  • Rotor copper loss
  • Friction, windage loss
  • Stray loss (misc losses)

Power flow

\[P_{\text{in}} \rightarrow P_{\text{SCL}} \rightarrow P_{\text{core}} \rightarrow P_{\text{RCL}} \rightarrow P_{\text{F\&W}} \rightarrow P_{\text{misc}} \rightarrow P_{\text{out}}\]

Where

  • \(P_{\text{SCL}}\) stator copper loss

  • \(P_{\text{core}}\) core losses

  • \(P_{\text{RCL}}\) rotor copper loss

  • \(P_{\text{F\&W}}\) friction and windage losses

  • \(P_{\text{misc}}\) stray losses

Air-gap power:

\[P_{\text{AG}} = P_{\text{in}} - P_{\text{SCL}} - P_{\text{core}}\]

Converted power:

\[P_{\text{conv}} = P_{\text{AG}} - P_{\text{RCL}}\]

Output power:

\[P_{\text{out}} = P_{\text{in}} - \left(P_{\text{SCL}} + P_{\text{core}} + P_{\text{RCL}} + P_{\text{F\&W}} + P_{\text{misc}}\right)\] \[P_{\text{out}} = P_{\text{conv}} - P_{\text{F\&W}} - P_{\text{misc}}\]

Efficiency:

\[\eta = \frac{P_{\text{out}}}{P_{\text{in}}}\]

Torque

\[\tau_{\text{ind}} = \frac{P_{\text{conv}}}{ {\omega}_m} = \frac{P_{\text{AG}}}{ {\omega}_{\text{sync}}}\]
\[P_{\text{SCL}} = 3 I^2_1 R_1\] \[P_{\text{AG}} = 3 I^2_2 \frac{R_2}{s}\] \[P_{\text{RCL}} = 3 I^2_2 R_2\] \[P_{\text{conv}} = 3 I^2_2 R_2 \left(\frac{1-s}{s} \right) = P_{\text{AG}} (1-s)\]

Maximum (Pullout) Torque

\[\tau_{\text{max}} = \frac{3 V^2_{\text{TH}}}{2 {\omega}_{\text{sync}} (R_{\text{TH}} + \sqrt{ R^2_{\text{TH}} + (X_{\text{TH}} + X_2)^2 }) }\]

The slip at maximum torque is

\[s_{\text{max}\ \tau} = \frac{R_2}{\sqrt{R^2_{\text{TH}} + (X_{\text{TH}} + X_2)^2}}\]

Where the equivalent Thévenin values are

\[Z_{\text{TH}} = \frac{jX_M (R_1 + jX_1)}{R_1 + j(X_1 + X_M)}\] \[V_{\text{TH}} = \frac{X_M}{\sqrt{R^2_1 + (X_1 + X_M)^2}} V_{\phi}\]

Type 1

Given:

  • Motor specs: frequency \(f_{se}\), poles \(P\), power \(P_{out}\), Y-connection
  • Slip \(s\)

Find:

  • Synchronous speed \(n_{\text{sync}}\) in rpm
  • Rotor speed \(n_m\) in rpm
  • Rotor frequency \(f_{re}\) in Hz
  • Shaft torque \({\tau}_{\text{load}}\)

1. Synchronous Speed \(n_{sync}\)

\[n_{\text{sync}} = \frac{120 f_{se}}{P}\]

2. Rotor Speed \(n_m\)

\[n_m = (1-s) n_{\text{sync}}\]

3. Rotor Frequency \(f_{re}\)

\[f_{re} = sf_{se}\]

4. Shaft Torque \({\tau}_{load}\)

\[{\tau}_{\text{load}} = \frac{P_{out}}{ {\omega}_m}\]

Type 2

Given:

  • Motor specs:
    • Voltage \(V_T\)
    • Frequency \(f_{\text{se}}\)
    • Power \(P_{\text{spec}}\)
    • Three-phase
  • Current \(I_L\)
  • Stator Power Factor \({PF}_S\)
  • Power losses \(P_{\text{SCL}},\ P_{\text{RCL}},\ P_{\text{FW}},\ P_{\text{core}},\ P_{\text{misc}}\)

Find:

  1. Air-gap power \(P_{\text{AG}}\)
  2. Power converted \(P_{\text{conv}}\)
  3. Output power \(P_{\text{out}}\)
  4. Efficiency \(\eta\)

1. Air-gap Power \(P_{\text{AG}}\)

First we need the input power:

\[P_{\text{in}} = \sqrt{3} V_T I_L \cos{\theta}\]

Note: \(\cos{\theta} = {PF}_S\).

\(P_{\text{SCL}},\ P_{\text{core}}\) are given. Replace below:

\[P_{\text{AG}} = P_{\text{in}} - P_{\text{SCL}} - P_{\text{core}}\]

2. Power Converted \(P_{\text{conv}}\)

\[P_{\text{conv}} = P_{\text{AG}} - P_{\text{RCL}}\]

3. Output Power \(P_{\text{out}}\)

\[P_{\text{out}} = P_{\text{conv}} - P_{\text{F\&W}} - P_{\text{misc}}\]

4. Efficiency \(\eta\)

\[\eta = \frac{P_{\text{out}}}{P_{\text{in}}}\]

Type 3

Given:

  • Motor specs:
    • Voltage \(V_{\phi}\)
    • Power \(P_{\text{rated}}\)
    • Poles \(P\)
    • Frequency \(f_{\text{se}}\)
    • Y-connection
  • Equivalent circuit values: \(R_1,\ X_1,\ R_2,\ X_2,\ X_M\)
  • Power losses: \(P_{\text{core}},\ P_{\text{F\&W}},\ P_{\text{misc}}\)
  • Ignoring \(R_C\) in the equivalent circuit
  • Slip

Find:

  1. Line current \(I_L\)
  2. Stator power factor \({PF}_S\)
  3. Rotor power factor \({PF}_R\)
  4. Rotor frequency \(f_{\text{re}}\)
  5. Stator copper losses \(P_{\text{SCL}}\)
  6. Air-gap power \(P_{\text{AG}}\)
  7. Converted power \(P_{\text{conv}}\)
  8. Induced torque \(\tau_{\text{ind}}\)
  9. Load torque \(\tau_{\text{load}}\)
  10. Efficiency \(\eta\)
  11. Motor speed \(n_m,\ {\omega}_m\)

1. Line Current \(I_L\)

Consider the equivalent impedance of the circuit \(Z_{eq}\):

  1. \(R_1,\ X_1\) are in series with (2 || 3).
  2. \(X_2,\ R_2,\ R_2 \left(\frac{1-s}{s}\right)\) are in series.
  3. \(X_M\) is in parallel with (2).

Sum (2) as a series, calculate its parallel with (3), then sum the result in series with (1). Let the resulting impedance be \(Z_{eq}\).

Let the impedances (2 || 3) be \(Z_F\). Write this value down, you need it later for \(P_{\text{AG}}\).

Given a Y-connection, calculate \(\frac{V_{\phi}}{\sqrt{3}}\) for the phase voltage. Then use Ohm’s Law for the line current:

\[I_L = I_A = \frac{\frac{V_{\phi}}{\sqrt{3}} \angle{0°}}{Z_{eq}}\]

The voltage is the reference phasor, hence the zero angle. The resulting current should have a negative phasor angle.

2. Stator Power Factor \({PF}_S\)

\[{PF}_S = cos {\theta}_s\]

Where \({\theta}_s\) is the phasor angle of the current \(I_L\).

If \({\theta}_s < 0\), say the power factor is lagging. It should always be negative for this type of problem.

3. Rotor Power Factor \({PF}_R\)

Consider the branch (2) of the circuit: \(X_2,\ R_2,\ R_2 \left(\frac{1-s}{s}\right)\). Find its impedance angle:

\[{\theta}_R = \arctan{\frac{s X_2}{R_2}}\]

Then use this angle for the power factor:

\[{PF}_R = cos {\theta}_R\]

Like \({PF}_S,\ {PF}_R\) should also be lagging.

4. Rotor Frequency \(f_{\text{re}}\)

\[f_{\text{re}} = s f_{\text{se}}\]

Usually, \(f_{\text{se}}\) is 50 or 60 Hz.

5. Stator Copper Losses \(P_{\text{SCL}}\)

\[P_{\text{SCL}} = 3 I^2_A R_1\]

6. Air-gap Power \(P_{\text{AG}}\)

\[P_{\text{AG}} = 3 I^2_A R_F\]

Where \(R_F\) is the real part of the impedance \(Z_F\) obtained in [1].

7. Converted Power \(P_{\text{conv}}\)

\[P_{\text{conv}} = P_{\text{AG}} (1-s)\]

8. Induced Torque \(\tau_{\text{ind}}\)

For the induced torque, we need \({\omega}_{sync}\):

\[n_{\text{sync}} = \frac{120 f_{\text{se}}}{P}\]

Where \(n_{\text{sync}}\) is in rpm.

\[{\omega}_{\text{sync}} = \frac{2 \pi n_{\text{sync}}}{60}\]

Where \({\omega}_{\text{sync}}\) is in rad/s.

Then we find the induced torque:

\[\tau_{\text{ind}} = \frac{P_{\text{AG}}}{ {\omega}_{\text{sync}}}\]

9. Load Torque \(\tau_{\text{load}}\)

We need the output power \(P_{\text{out}}\) and output speed \({\omega}_m\):

\[P_{\text{out}} = P_{\text{conv}} - P_{\text{F\&W}} - P_{\text{misc}}\]

For \({\omega}_m\):

\[n_m = n_{\text{sync}} (1-s)\] \[{\omega}_m = \frac{2 \pi n_m}{60}\]

Then the load torque is

\[{\tau}_{\text{load}} = \frac{P_{out}}{ {\omega}_m}\]

10. Efficiency \(\eta\)

\[\eta = \frac{P_{\text{out}}}{P_{\text{in}}} = \frac{P_{\text{out}}}{3 V_{\phi} I_A \cos{ {\theta}_S}}\]

11. Motor Speed \(n_m,\ {\omega}_m\)

We already got \(n_m\) and \({\omega}_m\) in [9].

Type 4

Given:

  • Motor specs:
    • Voltage \(V_{\phi}\)
    • Poles \(P\)
    • Frequency \(f_{\text{se}}\)
  • Power delivered to a load \(P_{\text{load}}\)
  • Motor speed \(n_m\)

Find:

  1. Slip \(s\)
  2. Induced torque \({\tau}_{\text{ind}}\)
  3. Motor speed \(n_m\), if the torque is doubled
  4. Power delivered to a load \(P_{\text{load}}\), if the torque is doubled

1. Slip \(s\)

We need the synchronous speed \(n_{\text{sync}}\):

\[n_{\text{sync}} = \frac{120 f_{\text{se}}}{P}\]

Then the slip is

\[s = \frac{n_{\text{sync}} - n_m}{n_{\text{sync}}}\]

2. Induced Torque \({\tau}_{\text{ind}}\)

Assuming no mechanical losses \(P_{\text{RCL}} = 0\) and \(P_{\text{conv}} = P_{\text{load}}\),

\[\tau_{\text{ind}} = \frac{P_{\text{conv}}}{ {\omega}_m}\]

Where

\[{\omega}_m = \frac{2 \pi n_m}{60}\]

3. Motor Speed \(n_m\)

Assuming low-slip region, the induced torque is directly proportional to slip. Therefore, if \(\tau_{\text{ind}}\) doubles, then \(s\) doubles too (approximate value).

Using \(n_{\text{sync}}\) and \(s\) as calculated in [1]:

\[n_m = n_{\text{sync}} (1- 2s)\]

4. Load Power \(P_{\text{load}}\)

If \(\tau_{\text{ind}}\) doubles, then

\[P_{\text{load}} = P_{\text{conv}} = 2\tau_{\text{ind}} {\omega}_{mm}\]

Where \({\omega}_{mm}\) is calculated from \(n_m\) in [3].